| vlsitechnology.org /IR drop /mn derivation |
Expression for Impact of Fixed Block Fraction mn on Power Delivery |
IR Drop
- IR drop problem
- Power delivery
- chip illustration
- 1W core power
- 2W core power
- 15% power straps
- 1W 30% blocks
- 2W 30% RAM, 20% analog
- upper power straps
- reducing impact
- 1W power best
- 2W power best
- 1W best 30% blocks
- 2W best RAM, analog
- summary of method
- conclusions
- example 1
- example 2
Derivations
A fixed block like a memory changes the power straps. The lower metal layers are typically blocked, while the higher layers can be routed over the top. In other fixed blocks like analog cells we can find that all layers are blocked to routing.
We consider the chip to be made up of standard cells and fixed blocks like memories which together have a certain area. The fraction of the core area taken up by the memories on each metal layer n is denoted by mn.
Metal-2 and metal-3 power straps stop the placement of anything else underneath them. If they occupy fractions p2 and p3 of the core side respectively,
| then the core area increases by | 1 | . |
| (1−p2)(1−p3) |
Consider the effect of a memory that occupies a fraction m′ of the core including power strap area. m′ = m(1-p2)(1-p3).
By lumping the metal layer as a single wire in the drawing on the right, it can be seen that the memory "bites" into the metal and reduces the amount available to convey power.
Without fixed blocks, the power supply metal area = px2. With fixed blocks the metal area = px2−pm′x2=px2(1−m′).
Thus the fraction pn of metal layer n which is used for power has to be scaled by (1-m′) or 1−m(1-p2)(1-p3).
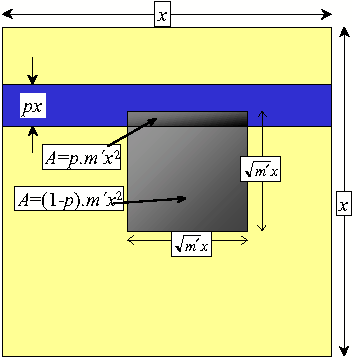
Picture showing impact of fixed block on effective width of metal power strap.