| vlsitechnology.org /IR drop /conductivity calculation |
Total Power Strap Conductivity Calculation |
IR Drop
- IR drop problem
- Power delivery
- chip illustration
- 1W core power
- 2W core power
- 15% power straps
- 1W 30% blocks
- 2W 30% RAM, 20% analog
- upper power straps
- reducing impact
- 1W power best
- 2W power best
- 1W best 30% blocks
- 2W best RAM, analog
- summary of method
- conclusions
- example 1
- example 2
Derivations
We define a factor L which is the parallel metal conductivity coefficient. That is, how much bigger the total metal conductivity will be than the reference metal conductivity due to multiple metal layers.
The power is delivered through the added power straps and through the metal-1 power rails in the standard cells. Firstly we consider the power that can be delivered through a power strap in metal layer n.
We already have an expression that links the power and the supply resistance Rsup.
| Pnom = | (Vcore−Vmin)×Vdd2 | × | 1 |
| Vddmin | Rsup |
We replace the term 1⁄Rsup by the conductance of the reference metal layer multiplied by
- the width coefficient kwn
- the conductivty coefficient kcn
- the scaling for the amount of metal layer n blocked to power straps
| 1 | = Gsup = | kwn⋅kcn⋅(1-mn(1-ka2p)(1-ka3p))⋅p⋅G |
| Rsup |
Each metal layer has a supply conductance given by this expression. Since these straps are in parallel, the total conductance is the sum of the individual values.
| Gsup (from straps) = | p⋅G⋅{kw1kc1(1-m1(1-ka2p)(1-ka3p)) + |
| kw2kc2(1-m2(1-ka2p)(1-ka3p)) + … + | |
| kw6kc6(1-m6(1-ka2p)(1-ka3p))} |
for a 6 layer metal process.
The other contributor to the power delivery is the standard cells' metal-1 power rails. In the absence of power straps, their conductance (which can be added to that of the power straps) will be
| Gsup (from cells) = | ps⋅G⋅{kc1(1-m1(1-ka2ps)(1-ka3ps)) |
In the presence of power straps, Gsup will be reduced by the fraction ps(1−p1) to
| Gsup (from cells) = | ps(1-p1)⋅G⋅{kc1(1-m1(1-ka2ps)(1-ka3ps)) |
The factor p1 equals kw1p. The total conductance Gsup is the sum of the two contributions
| Gsup = | G⋅{ps⋅kc1(1-m1(1-ka2p)(1-ka3p)) + |
| p⋅{kw1kc1(1-ps)(1-m1(1-ka2p)(1-ka3p)) + | |
| kw2kc2(1-m2(1-ka2p)(1-ka3p)) + … + | |
| kw6kc6(1-m6(1-ka2p)(1-ka3p))}} |
If we set
| L = | kw1⋅kc1⋅(1−ps)(1−m1(1−ka2p)(1−ka3p)) + |
| kw2⋅kc2(1−m2(1−ka2p)(1−ka3p)) + … + | |
| kw6⋅kc6(1−m6(1−ka2p)(1−ka3p)) |
then
| Gsup = | G⋅{ps⋅kc1(1-m1(1-ka2p)(1-ka3p))+p⋅L} |
Rearranging the expression for Pnom above and substituting Gsup for Rsup,
| Gsup = | Pnom × Vddmin | |
| (Vcore−Vmin)×Vdd2 | ||
which gives expressions for p and Pnom in terms of L.
| p = | { | Pnom × Vddmin | −ps⋅kc1(1−m1(1−ka2p)(1−ka3p)) | } | × | 1 |
| (Vcore−Vmin)×Vdd2×G | L |
| Pnom = | (Vcore−Vmin)×Vdd2×G | ×{ps⋅kc1(1−m1(1−ka2p)(1−ka3p))+pL} |
| Vddmin |
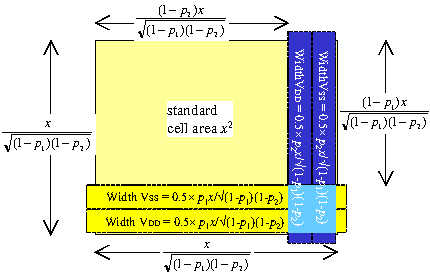
When the entire core is filled with standard cells, the fraction of metal-1 used for power is ps. If part of the core is taken up by power straps which block the standard cells, then these will use a smaller fraction of the metal-1 for power.
| The core side increases to x′ = |
|
. |
Fraction p1 of this is used by the metal-1 power strap, so fraction 1−p1 is used by the standard cells, and of this fraction ps is used by the standard cell power rails.
So in the presence of power straps, the fraction of metal-1 used for power rails must be scaled by ps(1−p1).
If we have an existing layout, we want to know the power delivery Pnom as a function of device specifications, technology characteristics and the amount of metal used for power straps.
We have this in the expression for Pnom below. Note that it depends on the value for Pnom itself through the term Vcore.
| Vcore = |
|
This means that we will need to iterate to the solution.
If we have a device spec including an estimate of the core power consumption, then we want to estimate the size of the power straps. We have this in the expression for p below. The width of the power straps in each metal layer n is kwn×p.
Note that if there are fixed blocks (any of mn>0), then the value of p depends on itself and we will have to iterate to the solution.