| vlsitechnology.org /IR drop /example 1 /die size impact |
Die Size Impact |
IR Drop
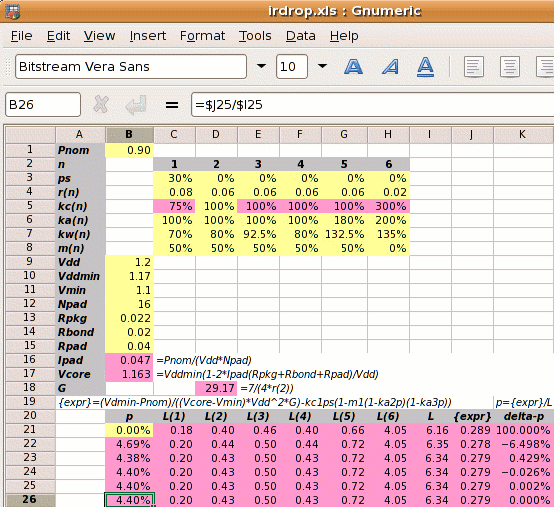
The steps to calculate the power strap allocation factor p have so far been similar to the previous text. The only real difference has been in the analysis of the supply widths and spacings, and how this affects the power strap width coefficient kw. Previously this was simply set to 80%.
The core size will be an integer number of cell rows and there will be an integer number of power straps. This means rounding up the theoretical numbers to get the IR drop adder.
Step 5: Calculate the new core size. If the initial core size estimate without power straps is x, then with power straps the core size becomes x′
| x′ = | x | = | x | = x+4.60% |
| √(((1−ka2p)(1−ka3p)) | 0.9560 |
This would increase the core side from 3.5mm up to 3.659mm.
The die size is built up from a precise calculation of the number of cell rows. We start with the
- height of a standard cell 4.4µm (80λ)
- size of the strap row which is 2 cell rows or 160λ
- starting core side of 3.498mm
The row height of 4.4µm gives 795.1 rows which we round up to 796 which in turn gives a core side of 3.502mm. We apply the equation above which gives a core side with power straps of 3.664mm.
| x′ = | 3.502 | = | 3.502 | = 3.664mm |
| √(((1−ka2p)(1−ka3p)) | 0.9560 |
This gives 832.6 cell rows which we round up to 833 rows. There were originally 796 rows, so the additional 37 cell rows are occupied by the power straps. Each strap rows is 2 cell rows tall, so there are 18.5 straps which we round up to 19, which increases the number of cell rows to 834. 834 rows gives a core side of 3.670mm which is actually an IR drop adder of
| 3.670-3.498 | = 4.89%. |
| 3.498 |
There are 19 straps which have a pitch of 44 cell rows. If they are spaced evenly, then 792 standard cell rows lie between the straps and 4 standard cell rows lie outside, so that the first strap row is row 3. We can use a spreadsheet as below to list the row numbers of each power strap.